Chapter 8: A Look Beyond – Evolving World Models

Note

This book is a work-in-progress! We’d love to learn how we can make it better, especially regarding fixing typos or sentences that are unclear to you. Please consider leaving any feedback, comments, or observations about typos in this google doc.

Attention

This chapter will extend the previously learned concepts from graphs to real world concepts.

8.1 Introduction

So far, we have uncovered many powerful concepts for modeling graphs and making changes to them. Using schema, We neatly packaged up data of a graph in a way that we can recover all its fundamental concepts – vertices and edges, and how they relate to one another. Using double-pushouts (DPO), we can edit an existing graph. With the capability to edit graphs, we can now model a number of graph-based scenarios such as, chemical reactions, and game design.

Schemas provide us with a language to talk about the concepts we wish to shed light on. The graph schema highlights edges and how they relate to nodes. Being remarkably general, schemas encourage us to be more ambitious and ask how can they model something non-graph based and more complex? For example, what if we were interested in talking about parts of a car or items in your kitchen? What parts go inside the other? What is wet and what is dry? And what items go with what and what items don’t go together? We would have to do quite a bit of mental book-keeping to talk in the language of graphs–

“For example, a bottle of Coca-Cola soda is a vertex and my refrigerator is another vertex… an edge between them means that the Coca-Cola soda is in the refridgerator,… but an edge between the soda and the vertex for a box of Mentos may mean that that the Mentos should never be put in the soda… edges take different meaning for each connection”

Note

If you put Mentos in a soda, it will explode.

So, graphs might not be a great idea to model my kitchen. Lucky for us, what we have learned so far have applications beyond graphs. The rest of this chapter is a simple demonstration of the use of schemas to modelling some complex scenarios.

8.2 Cube Configuration

Let’s start by simply extending the graph schema with another concept, like faces. Let us we want to model a cube. A face in a cube has four edges. So, along with Edge and Vertex and their relationship, the schema for a cube also consists of Face, and its relationship to edge(s). This schema has six relationships:

1. src and tgt from edges to vertices, and

2. top, bottom, left, right,from faces to edges.

Pause and ponder!

What can double pushouts (DPO) in this context model?

DPO rewriting in this context can model various transformations of a cube as if it were a packaging box.

In AlgebraicJulia, this schema can be expressed as follows:

@present SchCube(FreeSchema) begin
  Face::Ob
  Edge::Ob
  Vertex::Ob

  top::Hom(Face, Edge)
  right::Hom(Face, Edge)
  bottom::Hom(Face, Edge)
  left::Hom(Face, Edge)

  src::Hom(Edge, Vertex)
  tgt::Hom(Edge, Vertex)
end
to_graphviz(Sch3DShape)
@acset_type Typ3DShape(Sch3DShape)

We can see that the schema, SchCube, closely resembles the schema for a graph, SchGraph. More pointedly, SchCube extends SchGraph with the concept of a Face.

Extending schemas: From graphs to cubes

In AlgebraicJulia, inheritence of schemas can be programmed using <:. In the case of SchCube and SchGraph, this can be written as:

@present Sch3DShape(FreeSchema) <: SchGraph begin
  Face::Ob

  top::Hom(Face, Edge)
  right::Hom(Face, Edge)
  bottom::Hom(Face, Edge)
  left::Hom(Face, Edge)
end

We can model various configurations of a cube, akin to unfolding a cardboard box. For instance, using DPO rewriting, we could model the action of opening or closing the top of the box. This operation would involve redefining the relationships between the Faces and Edges objects to “remove” the connections that form the top face. Similarly, unfolding the cube into a flat layout would radically alter the connections between Faces, Edges, and Vertices to represent the cube in an unfolded state. Such transformations are powerful for visualizing and reasoning about the structural possibilities of boxes in three-dimensional space.

Let us say we want to have a cube representing a box with a birthday cake in it. When we deliver the cake to a friend, it starts off as closed. We can say that it’s closed by explaining how the faces, edges, and vertices are related to one another. In a cube, there are exactly six faces, which we can call f1, f2, f3, f4, f5, f6. Each face has exactly four edges, which we call the top, bottom, left, and right edges. Edges can also have names, such as e1, e2, e3, e4, .... If we want to say the top of edge of f1 is e1, then we can refer to the schema and express the the following piece of data:

top(f1) == e1

Similarly, we can say the bottom edge of f1 is e2 by saying:

bottom(f1) == e2

Edges, on the other hand, have exactly two vertices, the source and target. This is reminiscent of how we came to understand edges in a graph. The schema for both the Cube and the Graph have two morphisms, src and tgt, that map Edge to Vertex. So, if we would like to state what vertices bound the edge, e1, we can say

src(e1) == v1
tgt(e1) == v2

A closed box

We can create an instance of a cube, by associating data with the schema SchCube.

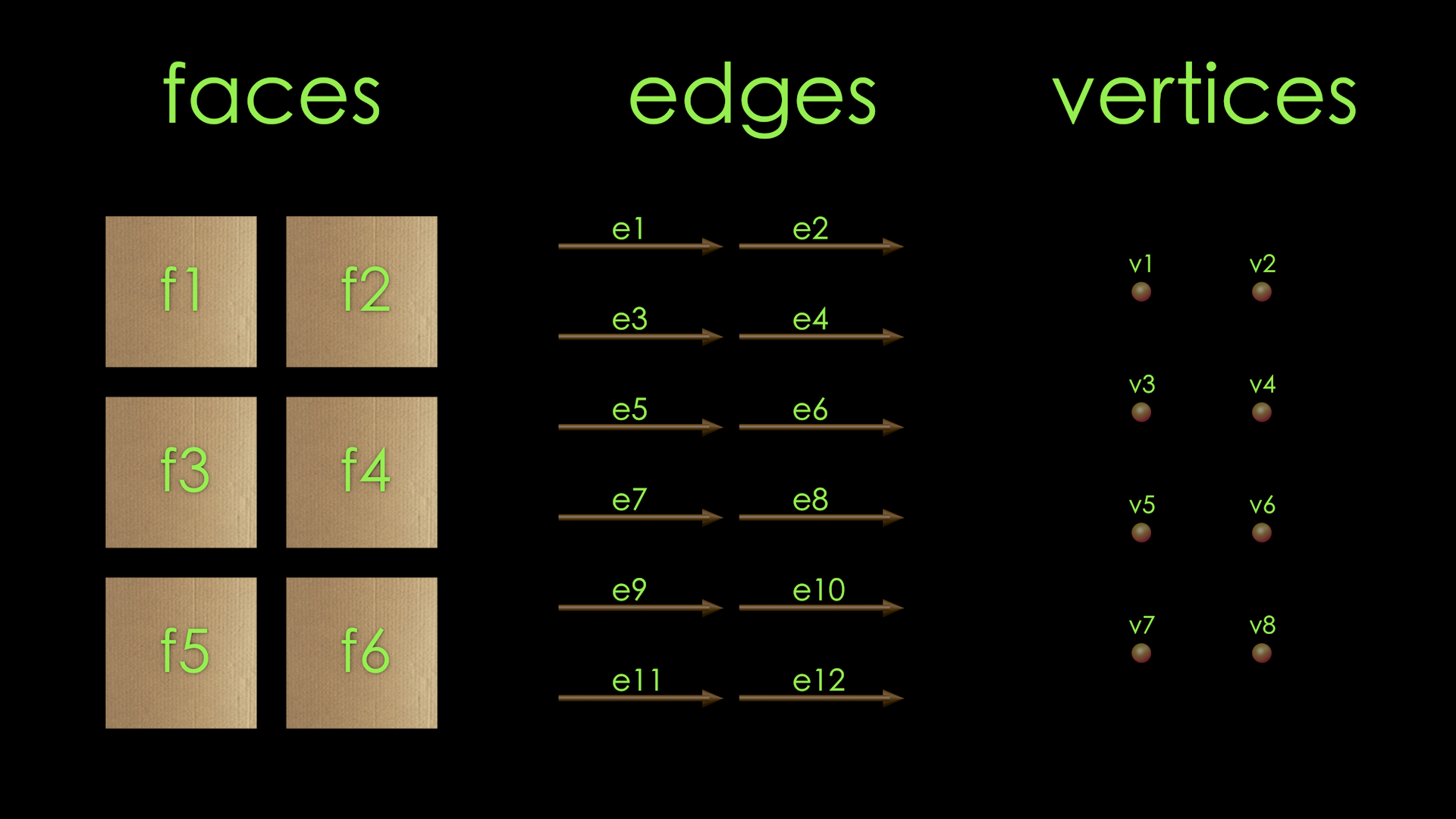
Fig. 1 A layout of the faces, edges, and vertices for our box.

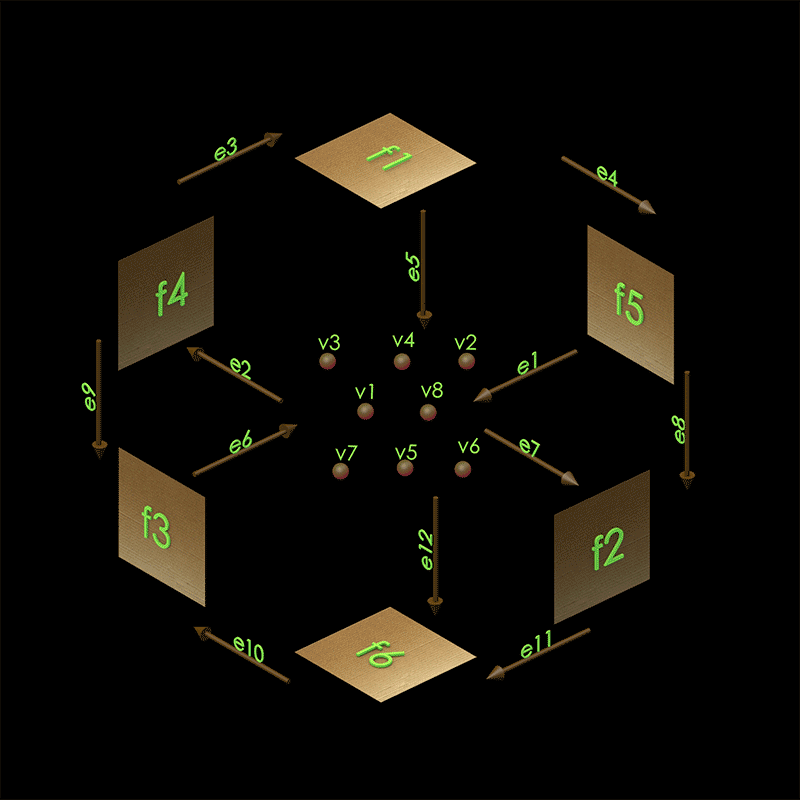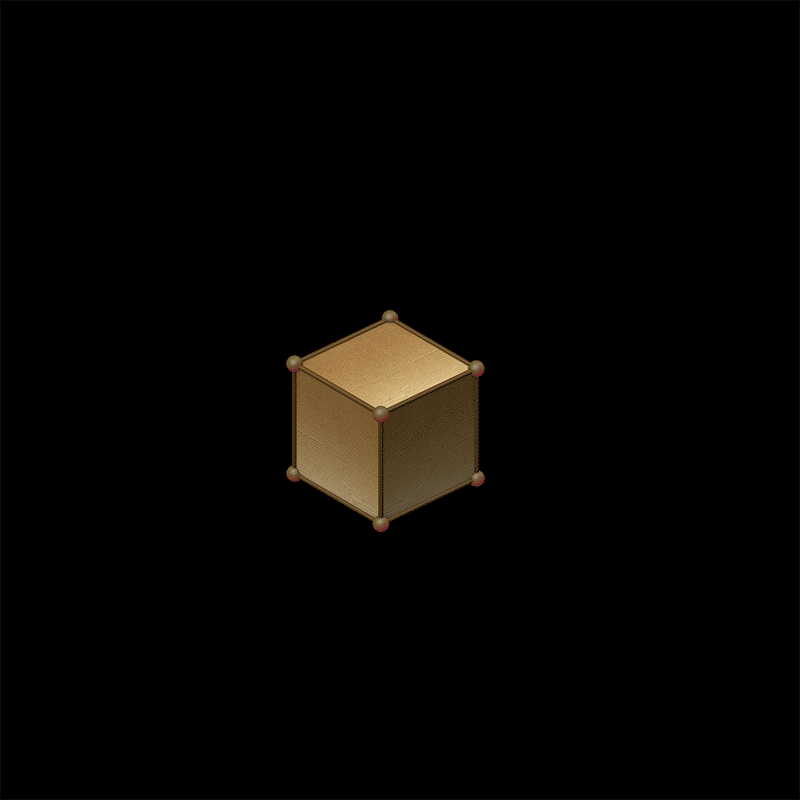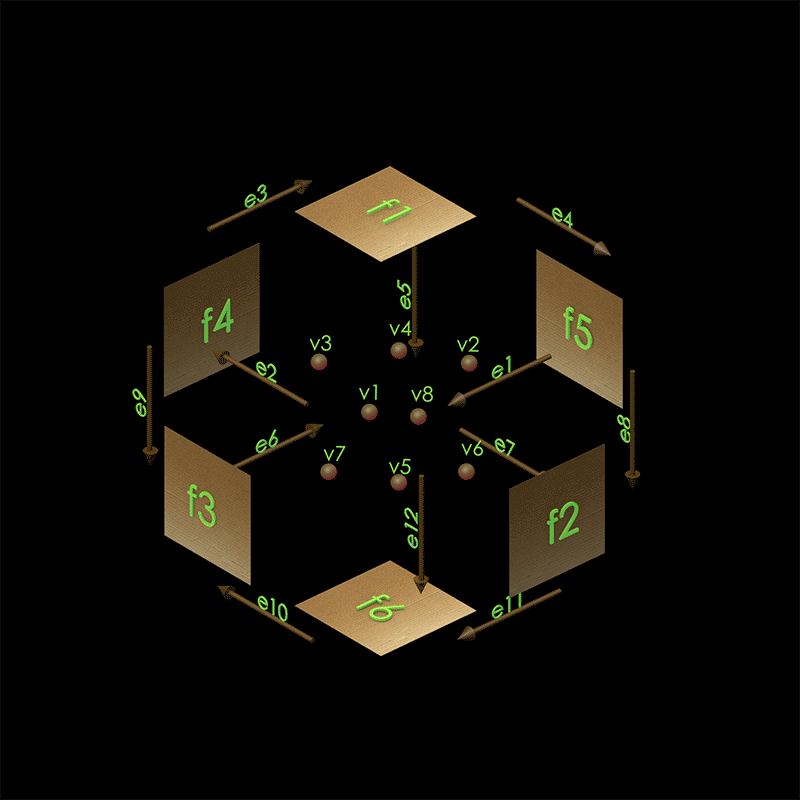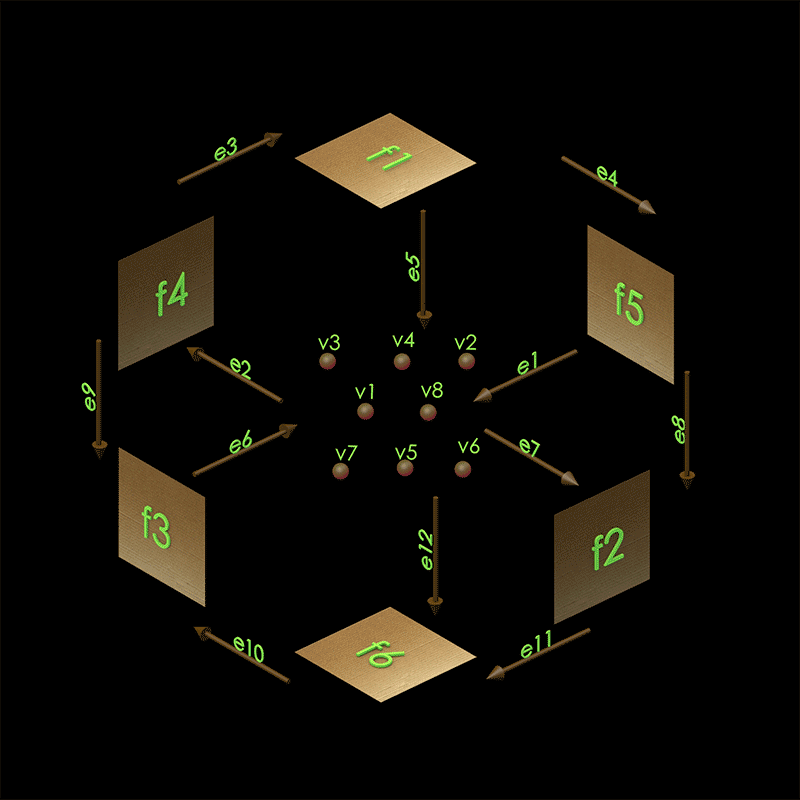
Fig. 2 The faces, edges, and vertices labeled for our box.

closedCube = @acset_colim ySchCube begin
  (f1, f2, f3, f4, f5, f6)::Face

  # top face (clockwise)
  top(f1) == top(f5)        # e1
  right(f1) == top(f2)      # e2
  bottom(f1) == top(f3)     # e3
  left(f1) == top(f4)       # e4

  # wall faces (clockwise)
  left(f2) == right(f3)     # e5
  left(f3) == right(f4)     # e6
  left(f4) == right(f5)     # e7
  left(f5) == right(f2)     # e8

  # bottom face (clockwise)
  top(f6) == bottom(f5)     # e9
  right(f6) == bottom(f2)   # e10
  bottom(f6) == bottom(f3)  # e11
  left(f6) == bottom(f4)    # e12

  # top vertices
  tgt(top(f1)) == src(right(f1))     # v1
  tgt(top(f1)) == src(right(f2))
  tgt(right(f1)) == src(bottom(f1))  # v2 
  tgt(right(f1)) == src(right(f3))
  tgt(bottom(f1)) == src(left(f1))   # v3 
  tgt(bottom(f1)) == src(right(f4))
  tgt(left(f1)) == src(top(f1))      # v4
  tgt(left(f1)) == src(right(f5))

  # bottom vertices
  tgt(top(f6)) == src(right(f6))     # v5
  tgt(top(f6)) == tgt(right(f2))
  tgt(right(f6)) == src(bottom(f6))  # v6
  tgt(right(f6)) == tgt(right(f3))
  tgt(bottom(f6)) == src(left(f6))   # v7 
  tgt(bottom(f6)) == tgt(right(f4))
  tgt(left(f6)) == src(top(f6))      # v8
  tgt(left(f6)) == tgt(right(f5))
end

This instance defines a box that looks like Fig. 1.

Opening a closed box

Now, once we deliver the birthday cake, we want be able to open the box so the birthday celebrant can enjoy their sweet treat. We can model this by designing a DPO rule that opens a face of the box. The rule looks for the top face of the cube, deletes it, and adds another face that is connected by only one edge to the rest of the cube.

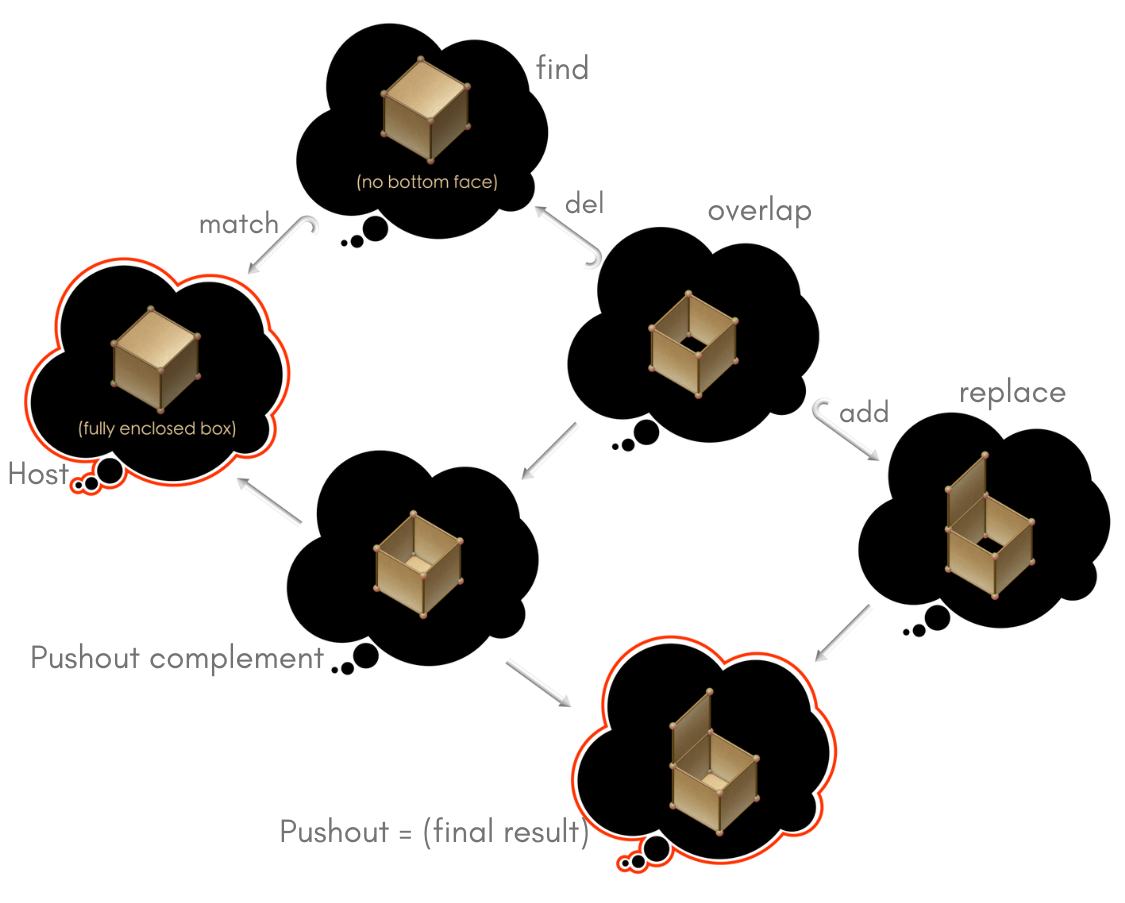
Fig. 3 The DPO rewrite rules for opening a closed box.

Opening a box: Coding the find and replace rule

The open box rule has the following Find, overlap, and Replace parts:

open_box = @migration(SchRule, Sch3DShape, begin
  find => @join begin
    (face, face1, face2, face3, face4)::Face

    # top edges
    top(face) == top(face1)
    right(face) == top(face2)
    bottom(face) == top(face3)
    left(face) == top(face4)

    # wall faces (clockwise)
    left(face1) == right(face2)
    left(face2) == right(face3)
    left(face3) == right(face4)
    left(face4) == right(face1)

    # top vertices
    src(right(face1)) == src(top(face1))
    src(right(face1)) == tgt(top(face4))
    src(right(face2)) == src(top(face2))
    src(right(face2)) == tgt(top(face1))
    src(right(face3)) == src(top(face3))
    src(right(face3)) == tgt(top(face2))
    src(right(face4)) == src(top(face4))
    src(right(face4)) == tgt(top(face3))

    # bottom vertices
    tgt(right(face1)) == src(bottom(face1))
    tgt(right(face1)) == tgt(bottom(face4))
    tgt(right(face2)) == src(bottom(face2))
    tgt(right(face2)) == tgt(bottom(face1))
    tgt(right(face3)) == src(bottom(face3))
    tgt(right(face3)) == tgt(bottom(face2))
    tgt(right(face4)) == src(bottom(face4))
    tgt(right(face4)) == tgt(bottom(face3))
  end
  overlap => @join begin
    (face1, face2, face3, face4)::Face
  end
  replace => @join begin
    (face1, face2, face3, face4, faceNew)::Face
    (edge1, edge2, edge3)::Edge

    # top edges
    top(faceNew) == top(face4)
    right(faceNew) == edge1
    bottom(faceNew) == edge2
    left(faceNew) == edge3

    # connect vertices of new edges
    src(edge1) == tgt(top(face4))
    tgt(edge1) == src(edge2)
    tgt(edge2) == src(edge3)
    tgt(edge3) == src(top(face4))

    # wall faces (clockwise
    left(face1) == right(face2)     # e5
    left(face2) == right(face3)     # e6
    left(face3) == right(face4)     # e7
    left(face4) == right(face1)     # e8

    # top vertices
    src(right(face1)) == src(top(face1))
    src(right(face1)) == tgt(top(face4))
    src(right(face2)) == src(top(face2))
    src(right(face2)) == tgt(top(face1))
    src(right(face3)) == src(top(face3))
    src(right(face3)) == tgt(top(face2))
    src(right(face4)) == src(top(face4))
    src(right(face4)) == tgt(top(face3))

    # bottom vertices
    tgt(right(face1)) == src(bottom(face1))
    tgt(right(face1)) == tgt(bottom(face4))
    tgt(right(face2)) == src(bottom(face2))
    tgt(right(face2)) == tgt(bottom(face1))
    tgt(right(face3)) == src(bottom(face3))
    tgt(right(face3)) == tgt(bottom(face2))
    tgt(right(face4)) == src(bottom(face4))
    tgt(right(face4)) == tgt(bottom(face3))
  end
  del => begin
    face1 => face1
    face2 => face2
    face3 => face3
    face4 => face4
  end
  add => begin
    face1 => face1
    face2 => face2
    face3 => face3
    face4 => face4
  end
end)
open_box_rule = make_rule(openBox, ySchCube)

Note: @migration is formatting the parts of the rule so that find, overlap, replace, del, and add are clearly identified.

The box never opens from underneath!

The rule looks for the top face of the cube, deletes it, and adds another face that is connected by only one edge to the rest of the cube.

The find part of the rule represents the condition that must be satisfied in order for the rule to be applied. In this case, we want to be able to open a face that is currently shut. A face is considered shut if it is connected to four other faces by four common edges. We can model this by defining a cube that has all but the bottom face. The bottom face is excluded because it is not relevant to the rule.

The overlap part tells us that all the wall faces are the same between find and replace.

The replace part of the rule represents the state in which the open face is connected to only one other face by a common edge that acts as the hinge to the open box. New edges and vertices are added to represent the disconnected edges.

This rule is also well-specified because it will only match on the top face of the box because it considers the orientation of the edges. That means the box will never open from underneath!

In summary, DPO rewriting can help us model various configurations of a box by manipulating the data associated with the SchCube schema.

8.3 Working in a Kitchen

This machinery can be used to not only represent geometric objects, but it can also the relationship of items in a kitchen.

Consider a schema for a kitchen world. This schema contains ideas about {Food, Egg, Bread, Cheese, BreadSlice, Counter, Kitchenware, Entity} and their subtyping relationships (e.g., Egg, Bread, Cheese, BreadSlice are Food) and spatial relationships (e.g., Counter is on an Entity, Kitchenware is on an Entity, and Food is on an Entity).

If you recall from Chapter 3, objects and morphisms in a schema are eventually mapped to sets and functions, respectively. This means that a relationship from Bread to Food says that all elements of Bread are a Food, and likewise, a morphism Food is on an Entity says that all elements of Food are on an Entity. This schema enforces a universal expectation about the types of objects and their arrangements while keeping track of what type of thing or relationship it is.

@present SchKitchen(FreeSchema) begin
  Entity::Ob

  Food::Ob
  food_in_on::Hom(Food, Entity)
  food_is_entity::Hom(Food, Entity)

  Kitchenware::Ob
  ware_in_on::Hom(Kitchenware, Entity)
  ware_is_entity::Hom(Kitchenware, Entity)

  Counter::Ob
  counter_is_entity::Hom(Counter, Entity)

  BreadLoaf::Ob
  bread_loaf_is_food::Hom(BreadLoaf, Food)
  BreadSlice::Ob
  bread_slice_is_food::Hom(BreadSlice, Food)
  Egg::Ob
  egg_is_food::Hom(Egg, Food)
  Cheese::Ob
  cheese_is_food::Hom(Cheese, Food)

  Knife::Ob
  knife_is_ware::Hom(Knife, Kitchenware)
  Plate::Ob
  plate_is_ware::Hom(Plate, Kitchenware)
end
to_graphviz(SchKitchen)

@acset_type Kitchen(SchKitchen)

yKitchen = yoneda(Kitchen, SchKitchen; cache=make_cache(Kitchen, SchKitchen, "Kitchen"))

DPO rewriting on kitchen arrangement can model transformations in the kitchen’s state, such as changing the arrangement of items. For example, using a DPO rewrite rule, we can simulate the action of combining cheese on a bread slice, thereby altering their relationships to reflect this new arrangement.

Put Cheese On Bread

Let us take as an example the action of putting cheese on bread. Following the same approach as the previous example, we can define find, replace, and overlap components of this rewrite rule.

put_cheese_on_bread = @migration(SchKitchen, begin
  find => @join begin
    cheese::Cheese
    slice::BreadSlice
  end
  overlap => @join begin
    cheese::Cheese
    slice::BreadSlice
  end
  replace => @join begin
    cheese::Cheese
    slice::BreadSlice
    cheese_is_food(cheese) == bread_slice_is_food(slice)  # become one
  end
end)
put_cheese_on_bread_rule = make_rule(put_cheese_on_bread, yKitchen)

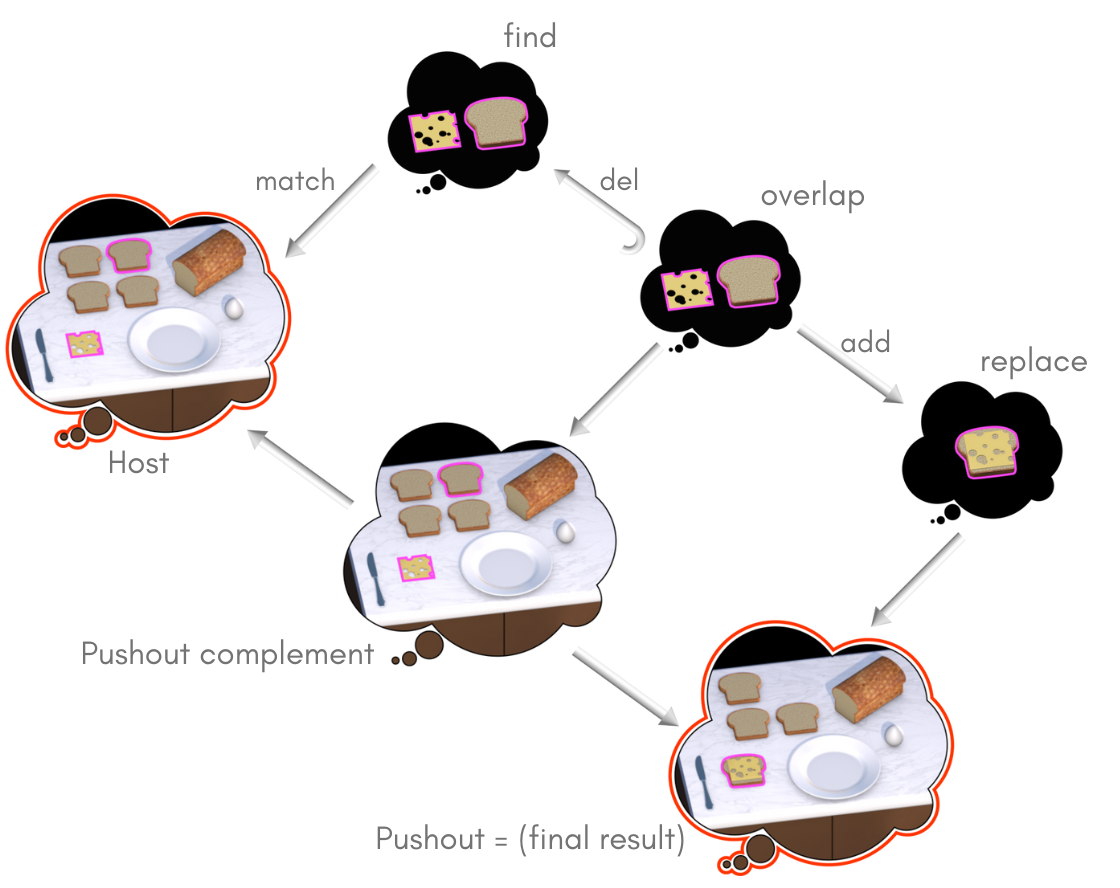
Fig. 4 The DPO rewrite rules for putting cheese on bread.

As we can see from this rule, we can model the concept of the bread slice and cheese becoming one by sending cheese to the same food element as bread_slice. Choosing to model the cheese being on bread as the fusion of cheese and bread is a knowledge engineering choice. This can easily have been represented using a relation about the cheese being on top of the bread. This further demonstrates the flexibility of DPO-rewriting rules.

Plate Slice

We can use the same idea to model a slice of bread being on a plate.

plate_slice = @migration(SchRule, SchKitchen, begin
  find => @join begin
    slice::BreadSlice
    plate::Plate
  end
  overlap => @join begin
    slice::BreadSlice
    plate::Plate
  end
  replace => @join begin
    slice::BreadSlice
    plate::Plate
    food_in_on(bread_slice_is_food(slice)) == ware_is_entity(plate_is_ware(plate))
  end
end)
plate_slice_rule = make_rule(plate_slice, yKitchen)

In this case, the bread slice and plate are mapped to the same entity. In the case of the bread slice, the function that does this mapping is tied to the food_is_on morphism and, in the case of plate, the function that maps it to entity is tied to the ware_is_entity morphism. This is effectively saying that the entity that the food is on is the same entity as the plate.

Pause and ponder

How will the double-pushout (DPO) square look like for this rule.

As we have seen, double-pushout rewriting can be used to update information that we know about the world both explicitly and implicitly. Explicitly, this is done by defining the rewrite rules and what we would like to change. Implicit information is captured by filling out the rest of the schema’s instances based on the explicit information. In robotics and AI planning, this accounting of both implicit and explicit effects on the world is called the frame problem and is a feature that must be carefully considered when designing planning languages for such purposes. This provides an elegant mathematical solution to this age-old problem.

8.4 Summary

Both examples illustrate the versatility of schemas and double-pushout rewriting in modeling transformations across different contexts. From the reconfiguration of physical structures like cubes to the dynamic arrangement of items in a kitchen, DPO rewriting provides a powerful tool for modeling and simulating changes in languages other than graphs. In particular, these concepts have shown promise in managing world states when doing task planning in robotics[1]. For the ambitious reader, we encourage you to not end your study here, but refer to advanced expositions of these topics[2][3].

Concluding words

Hope you had fun reading this book! If you feel inspired and convinced about relational thinking, and should you wish to delve deeper into the mathematics, we recommend you to the book [4] for a gentle yet technical introduction to category theory. We recommend you to the public forums Category Theory Zulip and localcharts for any help or further discussions on the content!

References

---

[1]

A Categorical Representation Language and Computational System for Knowledge-Based Planning. Angeline Aguinaldo, Evan Patterson, James Fairbanks, William Regli, & Jamie Ruiz. 2023 AAAI Fall Symposium on Unifying Representations for Robot Application Development. 2023.

[2]

Computational category-theoretic rewriting, 2023. Kristopher Brown, Evan Patterson, Tyler Hanks, James Fairbanks. Journal of Logical and Algebraic Methods in Programming.

[3]

Categorical data structures for technical computing, 2022. Evan Patterson, Owen Lynch, James Fairbanks. Compositionality.

[4]

Cheng, Eugenia. The joy of abstraction: An exploration of math, category theory, and life. Cambridge University Press, 2022.